从 SGD 到 Adam —— 6大常见优化算法总结

时间：2024-02-28 00:34:04    点击量：

论文 An overview of gradient descent optimization algorithms 的个人总结。

基于梯度下降的优化方法中，最朴素的 SGD 优化器采用的优化策略如下：

其他优化方法均基于对学习率 的改造。

Keywords：momentum， 全局学习率

如下图图 a 所示，当一个维度比另一个维度下降地明显更加急促时（经常是局部最优点），朴素 SGD 容易存在收敛极慢的问题。

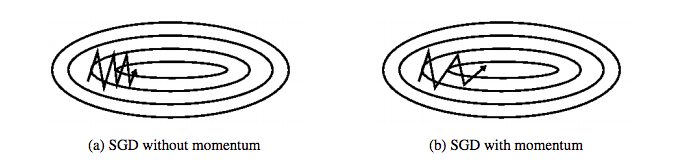
momentum（动量）的引入可以直观地较好处理这个问题，其在计算当前时刻的更新向量 时，引入了上一次更新向量 ，具体如下：

( 一般为0.9)

Keywords：momentum， 全局学习率，前瞻性预估

在momentum基础上，Nesterov accelerating 提供了一种颇有前瞻性的参数更新预估。

我们知道，动量将 引入了参数 的更新，因此 可以作为下一次更新后的参数的近似预估。据此计算梯度，是一种为参数更新引入前瞻性优化方法。具体为：

( 一般为0.9)

Kerwords: 不同参数自适应学习率，总体学习率不断衰减

Adagrad 为每个参数提供自适应的学习率，它可以为频率低的参数每次提供更大更新、为频率高的参数每次提供更小更新。正因为此，它十分适用于处理稀疏数据。

用 表示时刻 参数 的梯度：

则 SGD 对每个参数的更新为：

Adagrad对每个参数有自适应的学习率，其参数更新过程为：

（ 一般为1e-8）

是一个对角矩阵，其对角元素 是参数 截止时刻 的所有梯度的均方和。

Adagrad的最大优势是初始学习率（一般为0.01）设定后不用管，其可以为不同参数自适应地调整学习率。但同时，随着训练进行 是一个不断增长的过程，注定了其学习率是一个不断减小直至小到网络无法学习到新信息的过程。

Adadelta针对性地解决了Adagrad学习率过度衰减的问题。

Keywords: 自适应学习率，解决Adagrad学习率衰减过小的问题

Adadelta解决了Adagrad过度激进地衰减学习率的问题，不同于累加过去所有梯度的平方，它限制了累加的过去的梯度到一个固定窗口宽度 。

为进一步简化存储 个梯度的空间消耗，梯度和被递归地定义为之前所有梯度平方的均值的衰减，时刻 的梯度平方的均值被定义为：

( 一般取0.9)

因此参数更新向量为：

其分母为均方根（root mean squared, RMS）,因此也常写作：

本方法的作者进一步提出了更新单元不匹配的问题，时刻 的参数更新向量的平方的均值为：

有：

由于时刻 时 未知，因此采用前一时刻即 时刻的值来近似。则参数更新过程为：

可以看出，Adadelta事实上不需要设定初始学习率。

RMSprot 和 Adadelta 都是为了解决Adagrad的学习率消失问题而提出的。有趣的是，二者被独立提出，却殊途共归。RMSprop的参数更新过程为：

( 一般为0.001)

Adaptive Moment Estimation(Adam)是另一个为每个参数动态调整学习率的方法。正如其名，它同时估计了梯度的 first moment(mean, ) 和 second moment(variance, ):

（ 一般为0.9， 一般为0.999）

由于 , 初始化为0，且 , 均接近1，更新过程中尤其是初始阶段 , 倾向于0。

为解决这一问题，moment estimation 做了 bias-correct：

参数更新过程为：

稀疏数据则选择自适应学习率的算法；而且，只需设定初始学习率而不用再调整即很可能实现最好效果。

Adagrad, Adadelta, RMSprop, Adam可以视为一类算法。RMSprop 与 Adadelta本质相同，都是为了解决Adagrad的学习率消失问题。Adam 可视为添加了 bias-correction 和 momentum的 RMSprop。事实上，Adadelta, RMSprop, Adam在相似场景下表现也很相似。bias-correction 帮助 Adam 在优化后期略优于 RMSprop，因为此时梯度已经很稀疏。

目前来看，无脑用 Adam 似乎已经是最佳选择。