联系我们

CONTACT

手机：13988889999
电话：0898-88889999
ＱＱ：88889999
邮箱：admin@eyoucms.com
地址：海南省海口市玉沙路58号

优化算法_3

时间：2024-03-12 12:04:13 点击量：

置信域在当前最优结果附近定义一个范围，在这个范围内优化目标可以被近似为另一个函数

求解

$\\min_x f(x)$

一般在全空间中迭代产生若干点 $x_1,x_2,\\cdots$ ，是的 $f(x_i)$ 越来越小，从 $x_i$ 迭代生成 $x_{i+1}$ 基于两种方法

获得 $f(x)$ 下降方向并将x向着向下方向进行移动，类似于梯度下降

给定一个置信域 $D(x_i)$ ，求解约束

$\\min_xg(x)\\approx f(x)\\\\ x\\in D(x_i)$

使用二次方模型近似目标函数，但是如何约束置信域的大小？设置不合适可能导致收敛很慢或者过拟合

考虑的优化问题是Rosenbrock function

$f(x)=\\sum_{i=1}^{d-1}[w_i(x_{i+1}-x_i^2)^2+(x_i-1)^2],w_i\\geq 0$

全局最优为 $x=1^d$

解决了置信域大小难以约束的问题，置信域大小根据上一次迭代的表现决定，如果上一次表现存在较大提升，则采取更加激进的优化步长，反之减少优化步长

在 $x_k$ 处泰勒展开

$f(x_k+p)=f(x_k)+\ abla f(x_k)^T p+\\frac{1}{2}p^T\ abla^2 f(x_k)p+o(p^2)$

每一步迭代求解

$\\min_p f(x_k)+\ abla f(x_k)^T p+\\frac{1}{2}p^T \ abla ^2 f(x_k)p,\\parallel p\\parallel \\leq \\Delta_k$

$\\Delta_k$ 根据每次迭代的结果确定，先计算预测优化量和实际优化量的比值

$r_k=\\frac{f(x_k)-f(x_k+p)}{f(x_k)-m(p)}$

$r_k\\leq 0$ 说明优化目标与实际优化方向相反，如果 $r_k> 0$ ，判断条件( $\\Delta_M$ 是置信域的上街)

$r_k<0.25,\\Delta_{k+1}=0.25\\Delta_k$
$r_k>0.75,\\Delta_{k+1}=\\min(2\\Delta_k,\\Delta_M)$
否则保持置信域不变

随后还需要考察模型的提升程度，如果 $\\rho_k>0.1,x_{k+1}=x_k+\\rho_k$ ，否则 $x_{k+1}=x_k$

$\\min_p m_k(p)=f(x_k)+g_k^T p+\\frac{1}{2}p^T B_k p,\\parallel p\\parallel \\leq \\Delta_k\\\\ g_k^T=\ abla f(x)|_{x=x_k}\\\\ B_k=(\\frac{\\partial ^2 f(x)}{\\partial x_i \\partial x_j})_{i,j\\in[1,n]}$

拉格朗日对偶，假设feasible point是 $p^*$ ，于是需要满足

$\\exists \\lambda \\geq 0,s.t \\ (b+\\lambda I)p^*=-g,\\lambda (\\Delta - \\parallel p^*\\parallel)=0$

其中 $B+\\lambda I$ 是正定矩阵(如果f(x)是凸函数的话)

在置信域内，保留泰勒展开的一次项，沿着线性方向优化，首先使用线性项

$p_k^s=\\arg\\min_p f_k +g_k^T p,\\parallel p\\parallel \\leq \\Delta_k$

这里可以看出其实这种方法类似于梯度下降，选择的方向是梯度方向 $\ abla f_k$ ，选择的步长是

$p_k=-\ au_k \\frac{\\Delta_k}{\\parallel f(x_k)\\parallel}\ abla f_k\\\\ x_{k+1}=x_k + p_k$

$\\frac{\ abla f_k}{\\parallel \ abla f_k\\parallel}$ 将梯度归一化为一个大小为1的向量， $\ au_k$ 保证步长不超过置信域，选定步长约束为

$\ au_k=\\left\\{ \\begin{align*} &1\\quad \ abla f_k^T B_k \ abla f_k\\leq 0\\\\ &\\min(\\frac{\\parallel \ abla f_k\\parallel^3}{\\Delta_k \ abla f_k^T B_k \ abla f_k},1)\\quad else \\end{align*} \\right.$

将包含步长约束的步长带入二次展开中

$m(p_k)=m(\ au_k)=f_k -\ au_k\\frac{\\Delta_k}{\\parallel f_k\\parallel}\ abla f_k^T \ abla f_k +\\frac{1}{2}\ au_k^2\\frac{\\Delta_k^2}{\\parallel \ abla f_k\\parallel^2}\ abla f_k^T B_k \ abla f_k$

我们优化的目标是让 $m(\ au_k)\\leq f_k$ ，这样就得让第二项权重小于第三项(如果第三项权重为正的情况下)

这是一个拟二次函数，全局最优满足 $p^*=-B_k^{-1}\ abla f_k$ ，但是全局最优如果不在置信域中时，全局最优和置信域的交点并非一步最优迭代的结果

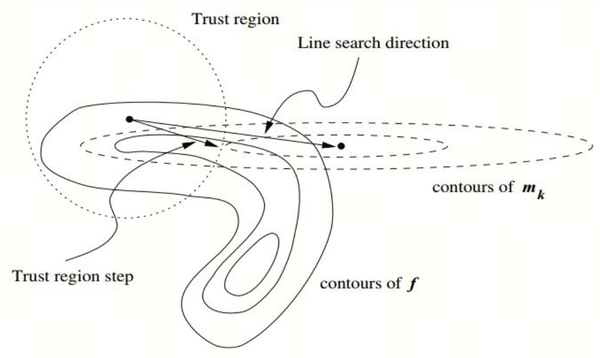
圆圈表示的是置信域，虚线表示的是二次展开的等高线，实线表示的是真实函数的等高线，可以看到Trust Region Step和Line Search direction(指向二次展开的最低点)存在区别，因此需要对Line Search Step进行一些修正

真实的最优步长具有如下特点

置信域很小时，接近梯度方向
原理泰勒展开的中心，接近无约束 $p^*$ 连线方向

使用torch自动求导机制，希望使用GPU增加并行度，比如

a = torch.tensor(1.0,requires_grad = True).cuda()
b = torch.pow(a,2)
b.backward()
print(a.grad)

此时会显示a is not leaf，必须将张量定义写成

a = torch.tensor(1.0,requires_grad=True,device='cuda:0')

$f(x)=w_1(x_2-x_1^2)^2 +(x_1-1)^2$

梯度是

$\ abla f(x)=(4w_1x_1^3-4w_1x_1x_2+2x_1-2,2w_1(x_2-x_1^2))$

hessian矩阵是

$\ abla^2 f(x)=\\begin{pmatrix} 12wx_1^2-4wx_2+2,-4wx_1\\\\ -4wx_1,2w \\end{pmatrix}$

采取三种方式优化

策略梯度
迭代优化，直接求解二次展开全局最优解
置信域，求解二次展开全局优化在置信域内的最优解，并迭代置信域大小

0,0处的梯度 $(-2,0)$ ，hessian矩阵

$\\begin{pmatrix} 2,0\\\\ 0,2w \\end{pmatrix}$

$f(x_0)$

迭代优化

求解最优化问题

$f(x_1,x_2)=\\sum_{i=1}^2 a_i x_i +\\sum_{i=1}^2 \\sum_{j=1}^2 w_{ij}x_i x_j\\\\ \\frac{\\partial f}{\\partial x_1}=a_1 + 2w_{12}x_2 +2w_{11}x_1=0\\\\ \\frac{\\partial f}{\\partial x_2}=a_2 +2w_{12}x_1+2w_{22}x_2=0\\\\ -0.5\\begin{pmatrix} w_{11}, w_{12}\\\\ w_{21}, w_{22} \\end{pmatrix}^{-1}\\begin{pmatrix}a_1\\\\ a_2 \\end{pmatrix}$

对于二项分布(p,N)而言，它的分布函数为

$P(n)=p^n \ imes (1-p)^{N-n}\ imes \\frac{N!}{(N-n)!n !}$

考虑累计分布

$P(X\\leq k)=\\sum_{i=0}^k p^i \ imes (1-p)^{N-i}\ imes \\frac{N!}{(N-i)!i!}$

希望将其写成简单的形式，对于beta函数，定义(a,b均为整数)

$B(a,b)=\\int_0^1 t^{a-1}(1-t)^{b-1}dt\\\\ B(x;a,b)=\\int_0^x t^{a-1}(1-t)^{b-1}dt\\\\ I_x(a,b)=\\frac{B(x;a,b)}{B(a,b)}=\\sum_{i=a}^{a+b-1}\\frac{(a+b-1)!}{i!(a+b-1-i)!}x^i (1-x)^{a+b-1-i}$

因此累积概率分布写成

$P(X\\leq k)=I_{p}(0,k+1)=1-P(X>k)=1-I_p(k+1,N-k)=I_{1-p}(N-k,k+1)$

生成正态分布

一个随机变量是时间的函数，我们在时间域上进行n次采样 $t_1,t_2,\\cdots,t_n$ ，得到n维向量 $\\epsilon_1,\\epsilon_2,\\cdots ,\\epsilon_n$ ，如果这个n维向量满足n维高斯分布，那么这是一个高斯过程

如果是标准正态分布，并且n维向量之间独立同分布，那么n维向量满足

$P(z_1,z_2,\\cdots,z_n)=\\prod_{i=1}^n \\frac{1}{\\sqrt{2\\pi}}\\exp(-\\frac{1}{2}z_i^2)$

一般的情况，如果n维向量并不满足iid，记

$\\vec\\mu,\\sum$

分别为向量的期望和协方差，向量 $\\vec z$ 满足分布

$\\mathcal{N}(\\vec\\mu,\\sum)\ o f(x)=\\frac{1}{(2\\pi)^{\\frac{n}{2}}|\\sum|^{\\frac{1}{2}}}\\exp{-\\frac{1}{2}(x-\\mu)^T \\sum^{-1}(x-\\mu)}$

多元二次分布由均值和协方差函数共同确定，

对于高斯过程时间片 $t_1,t_2,\\cdots,t_k$ 上进行采样得到的随机向量 $x_{t_1},x_{t_2},\\cdots,x_{t_k}$ ，它满足高维高斯分布 $N(\\mu_k,\\sum_k)$

现在在新的时间片 $t_{k+1}$ ，采样得到的一个新随机变量 $x_{t_{k+1}}$ ，加入到原始随机变量向量中满足k+1维高斯分布 $N(\\mu_{k+1},\\sum_{k+1})$

机器学习任务希望根据输入的特征向量x预测标签y，我们希望预测标签概率的分布 $p(y|x)$ ，对于黑盒模型 $f(x)$ ，只能通过一些采样点 $x_1,x_2,\\cdots,x_n$ 下的采样结果 $f(x_1),f(x_2),\\cdots,f(x_n)$ 拟合出这个黑盒函数，记

$f(x_{1:k})=[f(x_1),f(x_2),\\cdots,f(x_k)]\\\\ x_{1:k}=[x_1,x_2,\\cdots,x_k]$

为采样向量，它满足k维高斯分布

$N(\\mu(x_{1:k}),\\sum({x_{1:k},x_{1:k}}))$

我们希望根据样本值求出正态分布的均值向量和协方差矩阵，协方差矩阵记为

$\\begin{pmatrix} Cov(x_1,x_1) & \\cdots & Cov(x_1,x_k)\\\\ Cov(x_2,x_1) & \\cdots & Cov(x_2,x_k)\\\\ \\cdots \\\\ Cov(x_k,x_1) & \\cdots & Cov(x_k,x_k) \\end{pmatrix}=\\begin{pmatrix} k(x_1,x_1) & \\cdots & k(x_1,x_k)\\\\ k(x_2,x_1) & \\cdots & k(x_2,x_k)\\\\ \\cdots\\\\ k(x_k,x_1) & \\cdots & k(x_k,x_k) \\end{pmatrix}$

k是核函数，也被称为协方差函数，需要满足

对称半正定矩阵
距离相近的样本点之间协方差应该尽量大

采用高斯核

$k(x_1,x_2)=\\alpha_0 \\exp(-\\frac{1}{2\\sigma^2}\\parallel x_1-x_2\\parallel^2)$

预测矩阵函数，简单的方法是映射到常数

$\\mu(x)=c$

建模均值向量和协方差矩阵后，可以根据多维正态分布预测 $f(x)$ 在任意点函数值，对于样本值 $x_{1:k}$ 和采样值 $f(x_{1:k})$ ，对于接下来预测的点x对应的函数值 $f(x)$ ，我们希望预测其数学期望和方差

$\\mu(x),\\sigma^2(x)$

令 $x_{k+1}=x$ ，加入到原先的随机变量向量中，变为 $f(x_{1:k+1})$ ，满足k+1维高斯分布

$\\begin{pmatrix} f(x_{1:k})\\\\ f(x_{k+1}) \\end{pmatrix}| N( \\begin{pmatrix} \\mu_{x_{1:k}}\\\\ \\mu_{x_{k+1}} \\end{pmatrix}, \\begin{pmatrix} K,k\\\\ k^T,k(x_{k+1},x_{k+1}) \\end{pmatrix} )\\\\ k=[k(x_{k+1},x_1),k(x_{k+1},x_2),\\cdots,k(x_{k+1},x_k)]$

K是先前k次采样的协方差矩阵，计算向量k和协方差矩阵都没有用到函数值

多维高斯分布的条件分布是一维分布

$f(x_{k+1})|f(x_{1:k})-N(\\mu,\\sigma^2)\\\\ \\mu=k^T K^{-1}(f(x_{1:k})-\\mu(x_{1:k}))+\\mu(x_{1:k})\\\\ \\sigma^2=k(x_{k+1},x_{k+1})-k^T K^{-1}k$

在前k个采样点都确定的情况下，显然 $\\mu,\\sigma$ 是 $x_{k+1}$ 的函数，贝叶斯优化基于探索-利用权衡最大化

$\\mu(x)+\\beta\\sigma(x)$

高斯过程回归可以用于拟合非线性模型

对于训练数据集 $D=(X,y)={(x_i,y_i|i=1,2,\\cdots,N)}$ ，给定输入 $X^*$ ，求出预测数据Y
$Y=K(X^*,X)K(X,X)^{-1}y$
K通过核函数得到

黑盒优化问题：函数的表达式位置，无法通过梯度下降方法求得梯度

输入：f(黑盒优化目标)，X(参数搜索空间) D(采样得到的数据集) M(对数据集D拟合得到的模型，本文中采用高斯模型) S(采集函数，在参数空间中选择新的采样点，添加到数据集中)

算法：
从参数搜索空间中采样获得原始数据集D
迭代若干步
对于任意输入x，标签y，计算当前数据集下输出产生对应标签的概率 $P(y|x,D)\\leftarrow FITMODEL(M,D)$
根据估算的分布采样新的数据点 $x_i\\leftarrow \\arg\\max_{x\\in S}S(x,p(y|x,D))$
计算采样点处的函数值 $y_i=f(x_i)$
将 $x_i,y_i$ 添加到数据集D中形成新的数据集

关键是根据数据集D推断它的分布和从采集函数获取下一个数据点

计算协方差和均值，输入记为

$\\hat x=(x_1,x_2,\\cdots,x_n),\\hat y=(y_1,y_2,\\cdots,y_n)$

输入x和输出y之间被建模为正态分布 $p(y|x;D)=\\mathcal N (y|\\hat \\mu,\\hat \\sigma^2)$ ，计算正态分布的参数需要用到高斯过程回归

优化目标

$f(x):\\mathcal{X}\ o \\R$

观测值

$y_t=f(x_t)+\\epsilon\\ \\epsilon|N(0,\\sigma^2)$

贝叶斯优化的目标是找到一组序列 $x_1,x_2,\\cdots$ 使得趋近于优化目标，实际上迭代序列中的每一个元素都通过优化另一个优化目标实现

$x_t=\\arg\\max_{x\\in \\mathcal X}\\alpha_t (x)$

$\\alpha_t$ 被称为acquisition function，这个函数的选择要容易优化并且足够近似原本优化目标，这里牵涉到探索-利用均衡

希望尽可能探索没有探索的点(覆盖全参数空间)——探索
基于已经观察的结果，选择距离优化目标更近的点——利用

使用Gaussian Process建模这一过程，对于已经得到的探索序列 $x_1,x_2,\\cdots,x_t$ ，建模其均值 $\\mu_{t-1}(x)$ 和方差 $\\sigma_{t-1}(x)$ ，分别用于利用和探索

代理函数的作用是给样本点内每个样本打分，代理函数依据之前得到的样本点采样获得

获得(采集)函数根据打分返回最佳的采集样本，新的样本生成新的代理函数

GP-UCB

选择的迭代方式是

$x_t=\\arg\\max_{x\\in \\mathcal X}\\alpha_t (x)=\\arg\\max_{x\\in \\mathcal X}\\mu_{t-1}(x)+\\beta_t^{\\frac{1}{2}}\\sigma_{t-1}(x)$

$\\beta_t$ 在迭代时可以看成一个常数

有n个物品 $item_i,i=1,2,\\cdots,n$ ，每个物品具有一个被用户转化的概率p，记作
$f(k;p_i)=\\left\\{ \\begin{aligned} p_i,k=1\\\\ 1-p_i,k=0 \\end{aligned} \\right.$
转化率在推荐系统中可以视为用户的点击
推荐系统中涉及探索-利用问题，对于已经探索得到的点击序列，如果推荐点击过的商品，视为利用，反之视为探索，注意概率对于用户是不可见的，用户只能获得每次饰演的结果
一个机器有k个摇臂，投入一枚硬币，摇下第i个摇臂，返回 $x_i$ 奖励， $x_i$ 是一个随机变量，希望找到一种方法得到更多奖励

实际的模型用的是高斯过程回归，给定特征矩阵 $X$ 和标签y，建模高斯过程

$model=GaussianProcess(X,y)$

调用model.predict(X)获取高斯模型对于样本的预测

Upper Confidence Bound(UCB)

定义获得函数为

$\\alpha (x,\\lambda)=\\mu(x)+\\lambda \\sigma(x)$

均值体现出利用，方差体现出探索

PI(Probability of improvement)

定义利用函数

$u(x)=\\left\\{ \\begin{aligned} &0,f(x)> f^\\prime\\\\ &1,f(x)\\leq f^\\prime \\end{aligned} \\right.\\\\ f^\\prime是当前已知的采样点最小值$

最小化问题中只有 $f(x)$ 不大于 $f^\\prime$ 就有奖励，利用函数定义为

$\\alpha_{PI}(x)=E[u(x)|x,D]=\\Phi(f^\\prime,\\mu(x),K(x,x))$

实际上对于候选集中每一个采样点x，我们估算 $p(u(x)>0)$ 的概率(可能比现有结果更优的概率)，候选集中每个点的函数值 $f(x)$ 满足高斯分布

$f(x)|\\mathcal N(\\mu(x),\\sigma^2(x))$

假设 $z$ 满足标准正态分布 $\\mathcal N(0,1)$ ，那么 $f(x)=\\mu(x)+\\sigma(x)\ imes z$ 满足均值为 $\\mu(x)$ ，方差为 $\\sigma^2(x)$ 的正态分布，利用函数写成

$u(x)=\\max(f^\\prime-(\\mu(x)+\\sigma(x)z),0),z|\\mathcal N(0,1)$

则

$Pr(u(x)> 0)=Pr(f(x)\\leq f^\\prime)$

结合 $u(x)$ 的形式

$Pr(u(x)>0)=P(\\mu(x)+\\sigma(x)z< f^\\prime)=P(z< \\frac{f^\\prime-\\mu(x)}{\\sigma(x)})$

由于观测值 $f(x)$ 是一个随机变量，对应的获得函数也是一个随机变量，因此 $E[u(x)]$ 的大小实际上刻画了 $f(x)\\leq f^\\prime$ 的概率

$EI(x)=E[I(x)]=\\int_{-\\infty}^\\infty I(x)\\phi(z)dz$

$\\phi(z)$ 是标准正态分布，记住 $f(x)=\\mu(x)+\\sigma(x) z$ ，进一步写成

$\\begin{aligned} EI(x)&=\\int_{-\\infty}^\\infty \\max (f^\\prime -(\\mu(x)+\\sigma(x) z),0) \\phi(z) dz\\\\ &=\\int_{-\\infty }^{z_0}(f^\\prime - (\\mu(x)+\\sigma (x) z))\\phi(z) dz \\quad \\mu(x)+\\sigma(x) z_0=f^\\prime\\\\ &=\\int_{-\\infty}^{z_0}(f^\\prime -\\mu(x)) \\phi(z) dz + \\sigma(x)\\int_{-\\infty}^{z_0}z\\phi(z) dz \\end{aligned}$

本文使用 Zhihu On VSCode 创作并发布

【返回列表】