智能优化算法：麻雀搜索算法-附代码

时间：2024-06-24 13:59:54    点击量：

摘要：麻雀搜索算法(Sparrow Search Algorithm, SSA)是于2020年提出的。SSA 主要是受麻雀的觅食行为和反捕食行为的启发而提出的。该算法比较新颖，具有寻优能力强，收敛速度快的优点

建立麻雀搜索算法的数学模型，主要规则如下所述：

1. 发现者通常拥有较高的能源储备并且在整个种群中负责搜索到具有丰富食物的区域，为所有的加入者提供觅食的区域和方向。在模型建立中能量储备的高低取决于麻雀个体所对应的适应度值(Fitness Value)的好坏。
2. 一旦麻雀发现了捕食者，个体开始发出鸣叫作为报警信号。当报警值大于安全值时，发现者会将加入者带到其它安全区域进行觅食。
3. 发现者和加入者的身份是动态变化的。只要能够寻找到更好的食物来源，每只麻雀都可以成为发现者，但是发现者和加入者所占整个种群数量的比重是不变的。也就是说，有一只麻雀变成发现者必然有另一只麻雀变成加入者。
4. 加入者的能量越低，它们在整个种群中所处的觅食位置就越差。一些饥肠辘辘的加入者更有可能飞往其它地方觅食，以获得更多的能量。
5. 在觅食过程中，加入者总是能够搜索到提供最好食物的发现者，然后从最好的食物中获取食物或者在该发现者周围觅食。与此同时，一些加入者为了增加自己的捕食率可能会不断地监控发现者进而去争夺食物资源。
6. 当意识到危险时，群体边缘的麻雀会迅速向安全区域移动，以获得更好的位置，位于种群中间的麻雀则会随机走动，以靠近其它麻雀。

在模拟实验中，我们需要使用虚拟麻雀进行食物的寻找，由n只麻雀组成的种群可表示为如下形式：
$$X=?\begin{array}{cccc}{x}_1^1& x_1^2& ...& x_1^d\\ x_2^1& x_2^2& ...& x_2^d\\ ...& ...& ...& ...\\ x_n^1& x_n^2& ...& x_n^d\end{array}?\text{\hspace{1em}(1)}$$
其中，$d$ 表示待优化问题变量的维数，$n$ 则是麻雀的数量。那么，所有麻雀的适应度值可以表示为如下形式：
$$F_x=?\begin{array}{cccc}f([x_1^1& x_1^2& ...& x_1^d])\\ f([x_2^1& x_2^2& ...& x_2^d])\\ ...f([x_n^1& x_n^2& ...& x_n^d])\end{array}?\text{\hspace{1em}(2)}$$
其中，f 表示适应度值。

在 SSA 中，具有较好适应度值的发现者在搜索过程中会优先获取食物。此外，因为发现者负责为整个麻雀种群寻找食物并为所有加入者提供觅食的方向。因此，发现者可以获得比加入者更大的觅食搜索范围。根据规则(1)和规则(2)，在每次迭代的过程中，发现者的位置更新描述如下：
$$X_{i,j}^{t+1}=\{\begin{array}{l}{X}_{i,j}.exp(?\frac{i}{\alpha .ite{r}_{max}}),if{R}_2<ST\\ X_{i,j}+Q.L,if{R}_2\ge ST\end{array}\text{\hspace{1em}(3)}$$
其中，$t$ 代表当前迭代数，$j=1,2,3,...,d$。$ite{m}_{max}$
是一个常数，表示最大的迭代次数。$X_{ij}$表示第 $i$ 个麻雀在第$j$ 维中的位置信息。$\alpha \in (0,1]$是一个随机数。$R_2(R_2\in [0,1])$和 $ST(ST\in [0.5,1])$分别表示预警值和安全值。$Q$ 是服从正态分布的随机数。$L$ 表示一个 $1\times d$ 的矩阵，其中该矩阵内每个元素全部为 1。

当 $R2<ST$ 时，这意味着此时的觅食环境周围没有捕食者，发现者可以执行广泛的搜索操作。如果 $R2\ge ST$，这表示种群中的一些麻雀已经发现了捕食者，并向种群中其它麻雀发出了警报，此时所有麻雀都需要迅速飞到其它安全的地方进行觅食。

对于加入者，它们需要执行规则(3)和规则(4)。如前面所描述，在觅食过程中，一些加入者会时刻监视着发现者。一旦它们察觉到发现者已经找到了更好的食物，它们会立即离开现在的位置去争夺食物。如果它们赢了，它们可以立即获得该发现者的食物，否则需要继续执行规则(4)。加入者的位置更新描述如下：
$$X_{i,j}^{t+1}=\{\begin{array}{l}Q.exp(\frac{X_{worst}?X_{i,j}^t}{i^2}),ifi>n/2\\ X_P^{t+1}+|X_{i,j}?X_P^{t+1}|.A^{+}.L,otherwise\end{array}\text{\hspace{1em}(4)}$$
其中，$X_p$是目前发现者所占据的最优位置，$X_{worst}$则表示当前全局最差的位置。$A$表示一个 $1\times d$ 的矩阵，其中每个元素随机赋值为 1 或-1，并且 $A^{+}=A^T(A{A}^T{)}^{?1}$。当i >n/2 时，这表明，适应度值较低的第 i 个加入者没有获得食物，处于十分饥饿的状态，此时需要飞往其它地方觅食，以获得更多的能量。

在模拟实验中，我们假设这些意识到危险的麻雀占总数量的 10% 到 20%。这些麻雀的初始位置是在种群中随机产生的。根据规则(5)，其数学表达式可以表示为如下形式：
$$X_{i,j}^{t+1}=\{\begin{array}{l}{X}_{best}^t+\beta .|X_{i,j}^t?X_{best}^t|,if{f}_i>f_g\\ X_{i,j}^t+K.(\frac{|X_{i,j}^t?X_{worst}^t|}{(f_i?f_w)+\epsilon }),if{f}_i=f_g\end{array}\text{\hspace{1em}(5)}$$
其中，其中 $X_{best}$是当前的全局最优位置。$\beta$ 作为步长控制参数，是服从均值为 0，方差为 1 的正态分布的随机数。$K\in [?1,1]$是一个随机数，fi则是当前麻雀个体的适应度值。$f_g$和 $f_w$分别是当前全局最佳和最差的适应度值。$\epsilon$ 的常数，以避免分母出现零。

为简单起见，当 $f_i>f_g$表示此时的麻雀正处于种群的边缘，极其容易受到捕食者的攻击。$X_{best}$表示这个位置的麻雀是种群中最好的位置也是十分安全的。$f_i=f_g$时，这表明处于种群中间的麻雀意识到了危险，需要靠近其它的麻雀以此尽量减少它们被捕食的风险。$K$ 表示麻雀移动的方向同时也是步长控制参数。

算法流程

Step1： 初始化种群，迭代次数，初始化捕食者和加入者比列。

Step2：计算适应度值，并排序。

Step3：利用式（3）更新捕食者位置。

Step4：利用式（4）更新加入者位置。

Step5：利用式（5）更新警戒者位置。

Step6：计算适应度值并更新麻雀位置。

Step7：是否满足停止条件，满足则退出，输出结果，否则，重复执行Step2-6；

[1] Xue J , Shen B . A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems ence & Control Engineering An Open Access Journal, 2020, 8(1):22-34.

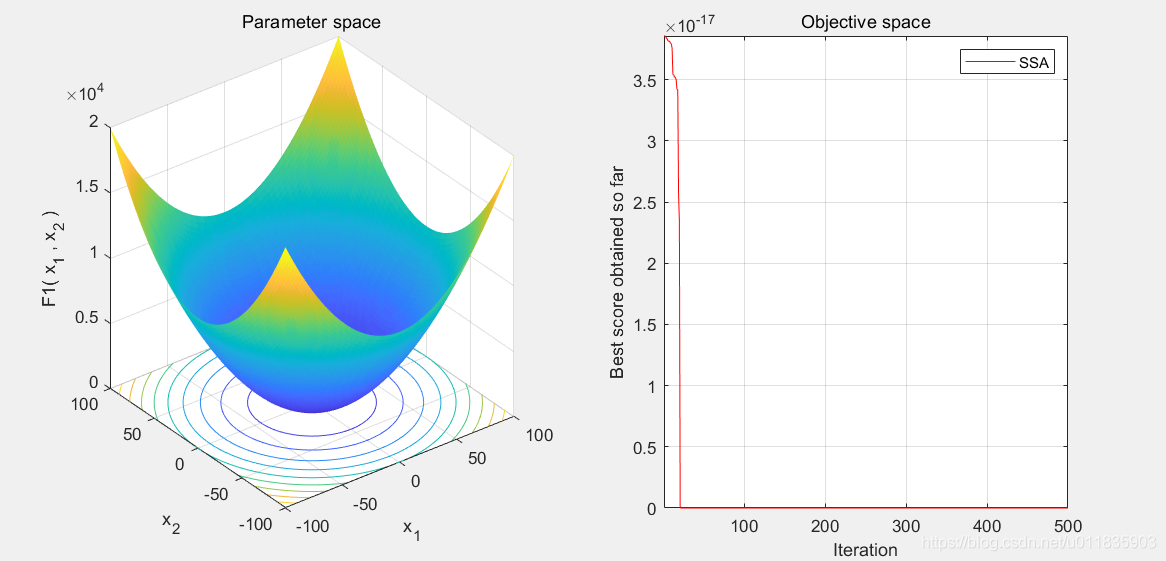
麻雀搜索算法
改进算法：

名称	说明或者参考文献
基于反向策略的麻雀搜索算法	原创
基于Tent混沌映射的麻雀搜索算法	原创
基于Logistic混沌映射的麻雀搜索算法	原创
基于Circle混沌映射的麻雀搜索算法	原创
基于Piecewise混沌映射的麻雀搜索算法	原创
基于Chebyshev混沌映射的麻雀搜索算法	原创
基于Sine混沌映射的麻雀搜索算法	原创
基于Singer混沌映射的麻雀搜索算法	原创
基于迭代混沌映射的麻雀搜索算法	原创
基于Sinusoidal混沌映射的麻雀搜索算法	原创
基于随机游走改进的麻雀搜索算法	原创
基于萤火虫改进的麻雀搜索算法	原创
基于精英反向策略的麻雀搜索算法1	原创
基于精英反向策略的麻雀搜索算法2	原创
基于levy飞行改进的麻雀搜索算法	原创
基于自适应t分布的麻雀算法	原创
混沌麻雀	[1]吕鑫,慕晓冬,张钧,王震.混沌麻雀搜索优化算法[J/OL].北京航空航天大学学报:1-10[2020-11-16].https://doi.org/10.13700/j.bh.1001-5965.2020.0298.
融合柯西变异和反向学习的改进麻雀算法	[1]毛清华,张强.融合柯西变异和反向学习的改进麻雀算法[J/OL].计算机科学与探索:1-12[2020-12-16].http://kns.cnki.net/kcms/detail/11.5602.tp.20201203.1601.006.html.
混合正弦余弦算法和Lévy飞行的麻雀算法(ISSA)	[1]毛清华,张强,毛承成,柏嘉旋.混合正弦余弦算法和Lévy飞行的麻雀算法[J/OL].山西大学学报(自然科学版):1-6[2021-04-09].https://doi.org/10.13451/j.sxu.ns.2020135.
基于 Sobol 序列和纵横交叉策略的麻雀搜索算法(SSASC)	[1]段玉先,刘昌云.基于 Sobol 序列和纵横交叉策略的麻雀搜索算法[J/OL]．计算机应用. https://kns.cnki.net/kcms/detail/51.1307.TP.20210525.1453.002.html
融合正余弦和柯西变异的麻雀搜索算法(SCSSA)	[1]李爱莲,全凌翔,崔桂梅,解韶峰.融合正余弦和柯西变异的麻雀搜索算法[J/OL].计算机工程与应用:1-11[2021-09-09].http://kns.cnki.net/kcms/detail/11.2127.TP.20210806.0937.008.html.
多策略融合的改进麻雀搜索算法(ISSA)	[1]付华,刘昊.多策略融合的改进麻雀搜索算法及其应用[J/OL].控制与决策:1-10[2021-09-09].https://doi.org/10.13195/j.kzyjc.2021.0582.
基于Logistic回归麻雀算法(MSSA)	[1]陈刚,林东,陈飞,陈祥宇.基于Logistic回归麻雀算法的图像分割[J/OL].北京航空航天大学学报:1-14[2021-09-26].https://doi.org/10.13700/j.bh.1001-5965.2021.0268.
自适应变异麻雀搜索优化算法(AMSSA)	[1]唐延强,李成海,宋亚飞,陈晨,曹波.自适应变异麻雀搜索优化算法[J/OL].北京航空航天大学学报:1-14[2021-09-27].https://doi.org/10.13700/j.bh.1001-5965.2021.0282.
混合策略改进的麻雀搜索算法(MSSA)	[1]张伟康,刘升,任春慧.混合策略改进的麻雀搜索算法[J/OL].计算机工程与应用:1-12[2021-08-05].http://kns.cnki.net/kcms/detail/11.2127.TP.20210721.0848.002.html.
融合多策略的改进麻雀搜索算法(ISSA)	[1]张晓萌,张艳珠,刘禄,张硕,熊夫睿.融合多策略的改进麻雀搜索算法[J/OL].计算机应用研究:1-8[2021-12-17].https://doi.org/10.19734/j.issn.1001-3695.2021.09.0412.
自适应t分布与黄金正弦改进的麻雀搜索算法(tGSSA)	[1]张伟康,刘升.自适应t分布与黄金正弦改进的麻雀搜索算法及其应用[J/OL].微电子学与计算机:1-8[2021-12-17].https://doi.org/10.19304/J.ISSN1000-7180.2020-0026.
分数阶麻雀搜索算法（FDSSA）	[1]江妍,马瑜,梁远哲,王原,李光昊,马鼎.基于分数阶麻雀搜索优化OTSU肺组织分割算法[J].计算机科学,2021,48(S1):28-32.
螺旋探索与自适应混合变异的麻雀搜索(SHSSA)	[1]陈功,曾国辉,黄勃,刘瑾.螺旋探索与自适应混合变异的麻雀搜索算法[J/OL].小型微型计算机系统:1-12[2021-12-24].http://kns.cnki.net/kcms/detail/21.1106.tp.20211214.1828.006.html.
改进搜索机制的单纯形法引导麻雀搜索算法（SMSSA）	[1]刘成汉,何庆.改进搜索机制的单纯形法引导麻雀搜索算法[J/OL].计算机工程与科学:1-9[2021-12-24].http://kns.cnki.net/kcms/detail/43.1258.TP.20211223.0930.002.html.
基于逐维高斯变异的混沌麻雀优化算法(ISSA)	[1]楚哲宇,唐秀英,谭庆,张清君.基于逐维高斯变异的混沌麻雀优化算法[J].自动化应用,2021(08):60-63.DOI:10.19769/j.zdhy.2021.08.019.
基于莱维飞行扰动策略的麻雀搜索算法(ISSA)	[1]马卫,朱娴.基于莱维飞行扰动策略的麻雀搜索算法[J].应用科学学报,2022,40(01):116-130.

算法相关应用matlab代码：

名称	说明或者参考链接
麻雀优化的BP神经网络（预测）	https://blog.csdn.net/u011835903/article/details/112149776
基于Tent混沌映射改进的麻雀搜索算法SSA优化BP神经网络（预测）	-
基于Sine混沌映射改进的麻雀搜索算法SSA优化BP神经网络（预测）	-
基于Logistic混沌映射改进的麻雀搜索算法SSA优化BP神经网络（预测）	-
麻雀优化的BP神经网络（分类）	https://blog.csdn.net/u011835903/article/details/112149394
基于麻雀搜索算法优化概率神经网络PNN的分类预测	https://blog.csdn.net/u011835903/article/details/111496232
基于麻雀搜索算法优化的Elman神经网络数据预测	https://blog.csdn.net/u011835903/article/details/111411127
基于麻雀搜索算法的极限学习机(ELM)分类算法	https://blog.csdn.net/u011835903/article/details/111177850
基于麻雀搜索算法的极限学习机(ELM)回归预测	https://blog.csdn.net/u011835903/article/details/111073635
基于麻雀算法优化的相关向量机RVM的分类算法	https://blog.csdn.net/u011835903/article/details/119005293
基于麻雀算法优化的相关向量机RVM回归预测算法	https://blog.csdn.net/u011835903/article/details/118998966
基于麻雀算法优化的核极限学习机（KELM）的分类算法	https://blog.csdn.net/u011835903/article/details/116851164
基于麻雀算法优化的核极限学习机(KELM)回归预测	https://blog.csdn.net/u011835903/article/details/116849032
基于麻雀搜索算法优化的广义回归神经网络(GRNN)预测	https://blog.csdn.net/u011835903/article/details/110941139
基于麻雀搜索算法优化的SVM数据分类预测	https://blog.csdn.net/u011835903/article/details/110523352
基于麻雀搜索的PID神经网络解耦控制算法	https://blog.csdn.net/u011835903/article/details/110437852
基于麻雀搜索优化K-means图像分割算法	https://blog.csdn.net/u011835903/article/details/109404281
基于麻雀算法优化的二维最大熵图像阈值分割	https://blog.csdn.net/u011835903/article/details/108214713
基于麻雀算法优化的最大熵多阈值分割	https://blog.csdn.net/u011835903/article/details/108203775
基于麻雀算法的二维Otsu图像阈值分割	https://blog.csdn.net/u011835903/article/details/108023193
麻雀算法优化的otsu多阈值分割	https://blog.csdn.net/u011835903/article/details/108019744
麻雀算法优化脉冲耦合神经网络的图像自动分割	https://blog.csdn.net/u011835903/article/details/112909060
基于麻雀算法优化的Tsallis相对熵图像多阈值分割	https://blog.csdn.net/u011835903/article/details/113755585
基于麻雀搜索算法与双伽马校正的图像自适应增强算法	https://blog.csdn.net/u011835903/article/details/109330643
基于麻雀搜索算法与非完全beta函数的自适应图像增强算法	https://blog.csdn.net/u011835903/article/details/109313513
基于麻雀搜索算法PID参数优化	https://blog.csdn.net/u011835903/article/details/109306387
基于麻雀搜索算法的TSP问题求解	https://blog.csdn.net/u011835903/article/details/109587929
基于麻雀搜索算法无线传感器网络(WSN)覆盖优化	https://blog.csdn.net/u011835903/article/details/109262039
基于麻雀搜索算法的3D无线传感器网络（WSN）覆盖优化	https://blog.csdn.net/u011835903/article/details/113834323
基于麻雀搜索的LMS自适应滤波算法	https://blog.csdn.net/u011835903/article/details/110529694
基于麻雀搜索的路径规划算法	https://blog.csdn.net/u011835903/article/details/109100220
基于麻雀搜搜算法的积分计算算法	https://blog.csdn.net/u011835903/article/details/114330697
基于麻雀搜索算法的工程优化案例（3种）	https://blog.csdn.net/u011835903/article/details/114106139
基于麻雀算法改进的随机森林回归预测算法（SSA-RF）	https://blog.csdn.net/u011835903/article/details/121860633
基于麻雀算法改进的随机森林分类算法（SSA-RF）	https://blog.csdn.net/u011835903/article/details/121860734
麻雀算法改进的深度极限学习机DELM的预测（SSA-DELM）	https://blog.csdn.net/u011835903/article/details/123115147
麻雀算法改进的深度极限学习机DELM的分类（SSA-DELM）	https://blog.csdn.net/u011835903/article/details/123091238
基于麻雀算法优化的Renyi熵图像多阈值分割	https://blog.csdn.net/u011835903/article/details/108276355 原理一样只是优化算法部分原理为麻雀
基于麻雀算法优化的指数熵图像多阈值分割	https://blog.csdn.net/u011835903/article/details/108263933 原理一样只是优化算法部分原理为麻雀
基于麻雀算法优化的灰度熵图像多阈值分割	https://blog.csdn.net/u011835903/article/details/108243596 原理一样只是优化算法部分原理为麻雀
基于麻雀算法优化的对称交叉熵图像多阈值分割	https://blog.csdn.net/u011835903/article/details/108241032 原理一样只是优化算法部分原理为麻雀
基于麻雀算法优化的最小交叉熵图像多阈值分割	https://blog.csdn.net/u011835903/article/details/108240562 原理一样只是优化算法部分原理为麻雀
基于麻雀算法优化的二维最大熵图像阈值分割	https://blog.csdn.net/u011835903/article/details/108214713 原理一样只是优化算法部分原理为麻雀
基于麻雀算法的二维Otsu图像阈值分割	https://blog.csdn.net/u011835903/article/details/108023193 原理一样只是优化算法部分原理为麻雀
基于麻雀搜索算法的同步优化特征选择	https://blog.csdn.net/u011835903/article/details/121103001
基于麻雀算法的投影寻踪模型(SSA-PP)	https://blog.csdn.net/u011835903/article/details/121120392
基于麻雀算法改进的无线传感器网络Dv-hop定位算法	https://blog.csdn.net/u011835903/article/details/121334401
基于麻雀算法的无人机航迹规划	https://blog.csdn.net/u011835903/article/details/122926764

麻雀搜索算法
改进算法：

名称	说明或者参考文献
基于反向策略的麻雀搜索算法	原创
基于Tent混沌映射的麻雀搜索算法	原创
基于Logistic混沌映射的麻雀搜索算法	原创
基于Circle混沌映射的麻雀搜索算法	原创
基于Piecewise混沌映射的麻雀搜索算法	原创
基于Chebyshev混沌映射的麻雀搜索算法	原创
基于Sine混沌映射的麻雀搜索算法	原创
基于Singer混沌映射的麻雀搜索算法	原创
基于迭代混沌映射的麻雀搜索算法	原创
基于Sinusoidal混沌映射的麻雀搜索算法	原创
基于随机游走改进的麻雀搜索算法	原创
基于萤火虫改进的麻雀搜索算法	原创
基于精英反向策略的麻雀搜索算法1	原创
基于精英反向策略的麻雀搜索算法2	原创
基于levy飞行改进的麻雀搜索算法	原创
基于自适应t分布的麻雀算法	原创
混沌麻雀	[1]吕鑫,慕晓冬,张钧,王震.混沌麻雀搜索优化算法[J/OL].北京航空航天大学学报:1-10[2020-11-16].https://doi.org/10.13700/j.bh.1001-5965.2020.0298.
混合正弦余弦算法和Lévy飞行的麻雀算法(ISSA)	[1]毛清华,张强,毛承成,柏嘉旋.混合正弦余弦算法和Lévy飞行的麻雀算法[J/OL].山西大学学报(自然科学版):1-6[2021-04-09].https://doi.org/10.13451/j.sxu.ns.2020135.

算法相关应用Python代码：

名称	说明或者参考文献
基于麻雀算法的SVM分类（SSA-SVM）	https://blog.csdn.net/u011835903/article/details/110523352
基于麻雀算法的SVM回归预测（SSA-SVM）	https://blog.csdn.net/u011835903/article/details/110630270
基于麻雀搜索算法的极限学习机(ELM)分类算法（SSA-ELM）	https://blog.csdn.net/u011835903/article/details/111177850
基于麻雀搜索算法的极限学习机(ELM)回归预测算法（SSA-ELM）	https://blog.csdn.net/u011835903/article/details/111073635
基于麻雀算法的无线传感器网(WSN)覆盖优化（SSA-WSN）	https://blog.csdn.net/u011835903/article/details/109262039
基于麻雀算法改进的随机森林分类算法（SSA-RF）	https://blog.csdn.net/u011835903/article/details/121860734
基于麻雀算法改进的随机森林回归预测算法（SSA-RF）	https://blog.csdn.net/u011835903/article/details/121860633